2022
We present a toy informational model of quantum gravity in which physical laws are emergent consequences of a maximally compressed informational universe. Observers are treated as compressed Gaussian wavefunction structures, whose probability of existence is proportional to their informational complexity. Particles are generated from a probabilistic field influenced by all observers, and candidate trajectories are selected according to a compressibility-based cost function. Through this selection process, smooth, deterministic motion naturally emerges, providing an informational explanation for inertia. The simulation demonstrates that law-like, predictable behavior arises from the statistical dominance of compressed observers, supporting the broader hypothesis that both Quantum Mechanics and General Relativity can be interpreted as emergent from optimal information compression.
The search for a unified theory of everything has been a central pursuit in modern physics. However, traditional approaches often begin with a set of assumed fundamental laws. This paper proposes an alternative framework where the laws themselves are not fundamental but are emergent from a more primitive, informational substrate.
The key idea is that existence itself is biased toward compression. Observers are not passive; their probability of existing is directly tied to how efficiently their informational structure can be described. This leads to the following chain of reasoning:
Compression increases multiplicity: An observer that can be described with fewer bits can be described in vastly more ways within the underlying informational substrate.
Multiplicity increases probability: The more copies of an observer exist, the higher the probability that any given observer will be one of them.
Probability selects predictable worlds: Observers therefore overwhelmingly find themselves in worlds where their own informational structure is maximally compressible.
Predictability manifests as physical law: Smooth, regular, law-like behavior (e.g., inertia) is the kind of information that compresses best. Consequently, the laws of physics that we observe are not fundamental givens, but statistical artifacts of compression dominance.
In short: you observe smooth, predictable physical laws because only in such worlds can compressed observers proliferate and dominate the measure of existence. Quantum Mechanics, General Relativity, and others can be pictured as the most efficient compression algorithms.
An observer is defined as a compressed informational structure. In our 2D model, this structure is a parametric complex wavefunction, \(\psi(x,t)\), representing a soft disk or Gaussian shell:
\[\psi(x,t) = A \exp\big(-2\sigma^2 (r - R)^2\big)\,\exp\big(-i(\omega t - \phi)\big)\]
Here, \(r = \|x - c\|\) is the radial distance from the center \(c\), \(A\) is the amplitude, \(R\) is the radius of the shell, \(\sigma\) is its width, \(\omega\) is its frequency, and \(\phi\) is its phase.
An observer emerges from the underlying random noise field by applying a filter. This is modeled by a Gaussian observer window, \(O_j(x)\), which smoothly weights the influence of particles based on their proximity to the observer’s center:
\[O_j(x) = \exp\big(-2\sigma_{\text{obs}}^2 \|x - c_j\|^2\big)\]
The random noise is represented by a large number of particles. These particles are not governed by forces but are probabilistically resampled from a total probability density function (PDF). This PDF is generated from the interference pattern of all observer wavefunctions:
\[P(x) = \big|\Psi_{\text{total}}(x,t)\big|^2 = \left|\sum_j \psi_j(x,t)\right|^2\]
Each step of the simulation involves resampling particles from this emergent field, which is a direct consequence of the collective influence of all observers.
The central prediction of the theory is the generation of deterministic motion through a selection process guided by informational compressibility. We model this as follows:
Particles are "softly" assigned to observers using weights proportional to both the observer’s filter function and the local probability density:
\[W_j(x) \propto O_j(x)\cdot |\psi_j(x)|^2\]
For each observer, a set of potential next positions (candidates) is generated based on the local particle distribution. Each candidate corresponds to a small perturbation in the observer’s wavefunction parameters, such as phase \(\phi\) or frequency \(f\). While the formal Everettian view would require consideration of all possible arrangements of information, this approximation via finite candidate sets is justified by computational tractability and the concentration of probability mass.
The choice among candidates is determined by an informational cost function derived from the principle of minimal description length (MDL). The change in description length when moving from state \(s_t\) to \(s_{t+1}\) is:
\[\Delta C_j = \mathcal{K}(s_{t+1}) - \mathcal{K}(s_t)\]
We approximate the compressibility cost function using the Shannon entropy of the change in velocity vector \(\Delta v\):
\[\text{Cost}_j(\Delta v) = H(\Delta v) \approx \Delta \phi^2 + \Delta f^2\]
The observer selects the candidate trajectory with the lowest cost. Continuity of velocity emerges because it is informationally optimal. In this framework, inertia is not a fundamental law but a by-product of the system’s bias toward minimal description length.
The simulation is implemented in Python and consists of several key classes:
Wavefunction: Represents the parametric Gaussian shell.
ObserverWindow: A Gaussian function used for soft assignment.
WavefunctionGravitySim: The main simulation class that computes total PDF, resamples particle positions, and uses candidate selection to implement informational inertia.
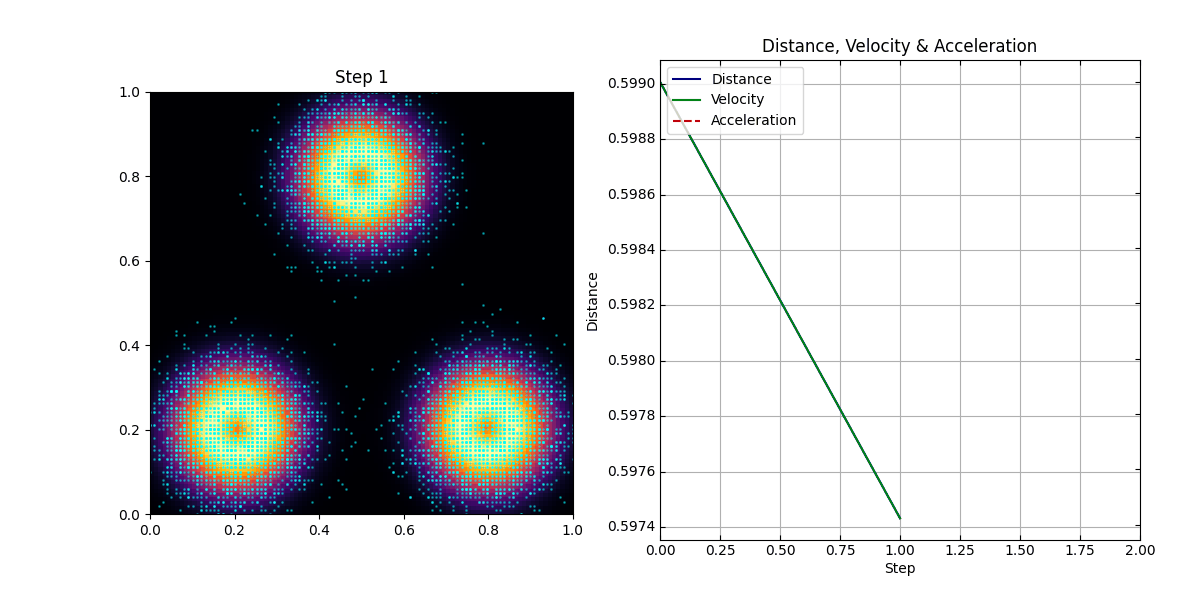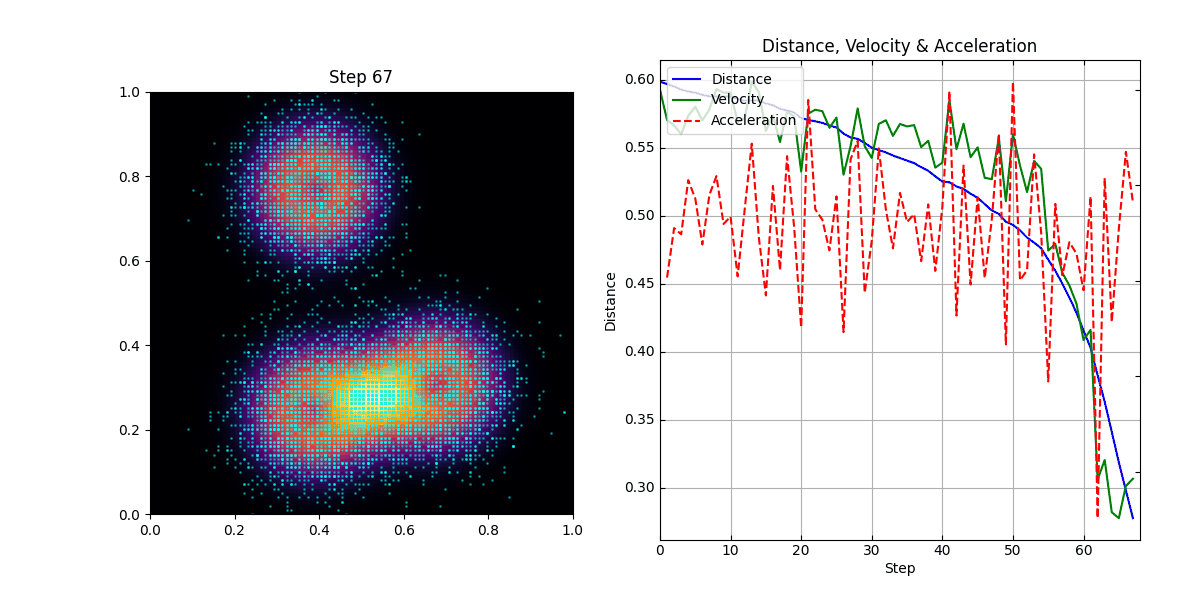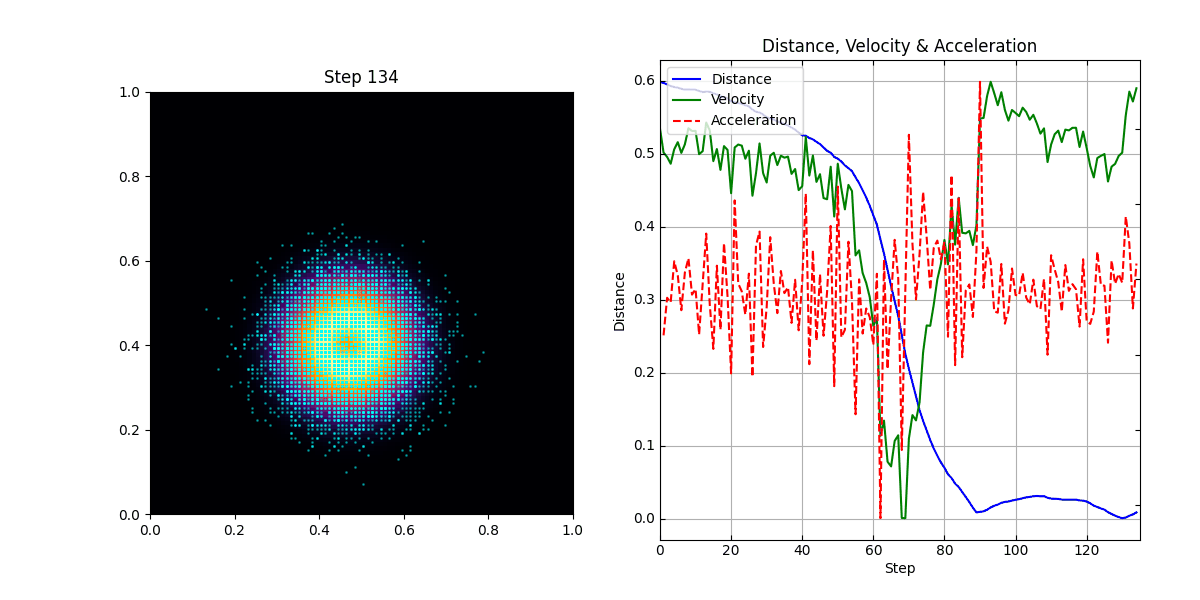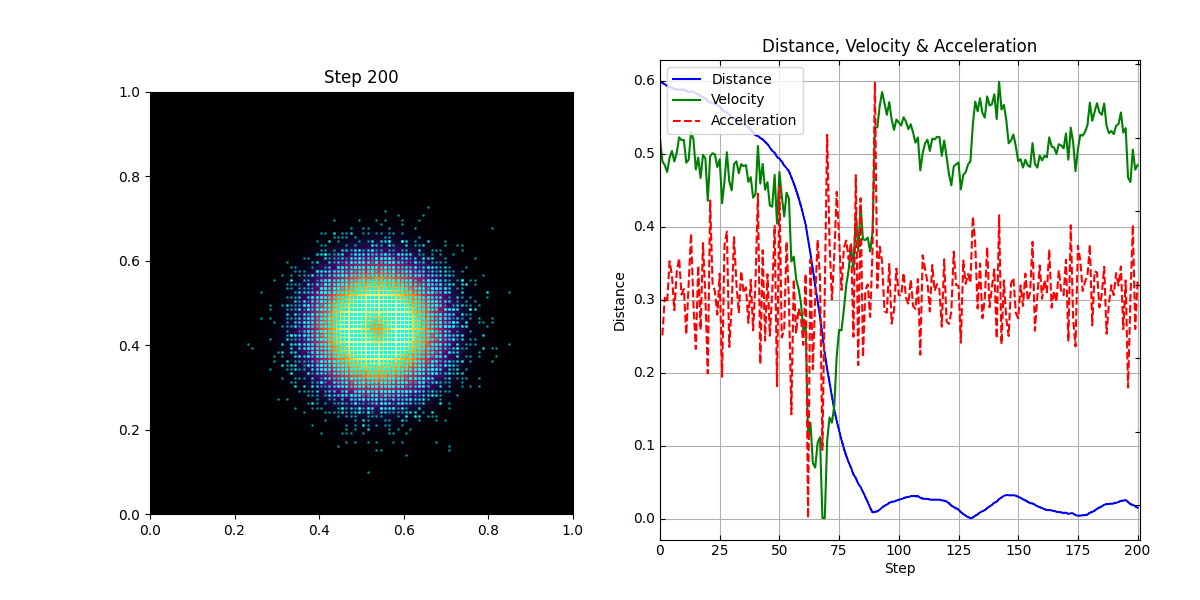
The simulation successfully demonstrates the emergence of inertial, law-like behavior. Observers, initially placed in a random configuration, quickly begin to move in smooth, predictable paths.
Trajectory Smoothness: Observed trajectories exhibit significantly lower variance compared to random baseline motion.
Entropy Rate of Motion: The Shannon entropy \(H(\Delta v)\) decreases over time as trajectories stabilize.
Compressibility Trend: The cumulative cost function \(\sum_t \text{Cost}_j(\Delta v_t)\) decreases monotonically.

This work supports the Compression–Existence Principle: the more compressible an observer, the more ways information can be arranged to describe them, and the higher their probability of existence. What we call the “laws of physics” are emergent regularities; they are selected because only such highly compressed observers dominate the measure of existence.
Future work will focus on extending this model to simulations in which both Quantum Mechanics and General Relativity emerge as the most probable compressible outcome of random selection and observer filters.