Introduction

In prior work, we demonstrated that probabilistic gravity and inertia emerge from the dominance of compressible trajectories of Gaussian blobs in a 2D particle field. While these blobs captured gravity-like attraction and emergent QM-like behavior, their fixed isotropic shapes limited the simulation’s ability to reproduce general relativistic geodesics, where matter dynamically shapes spacetime geometry.

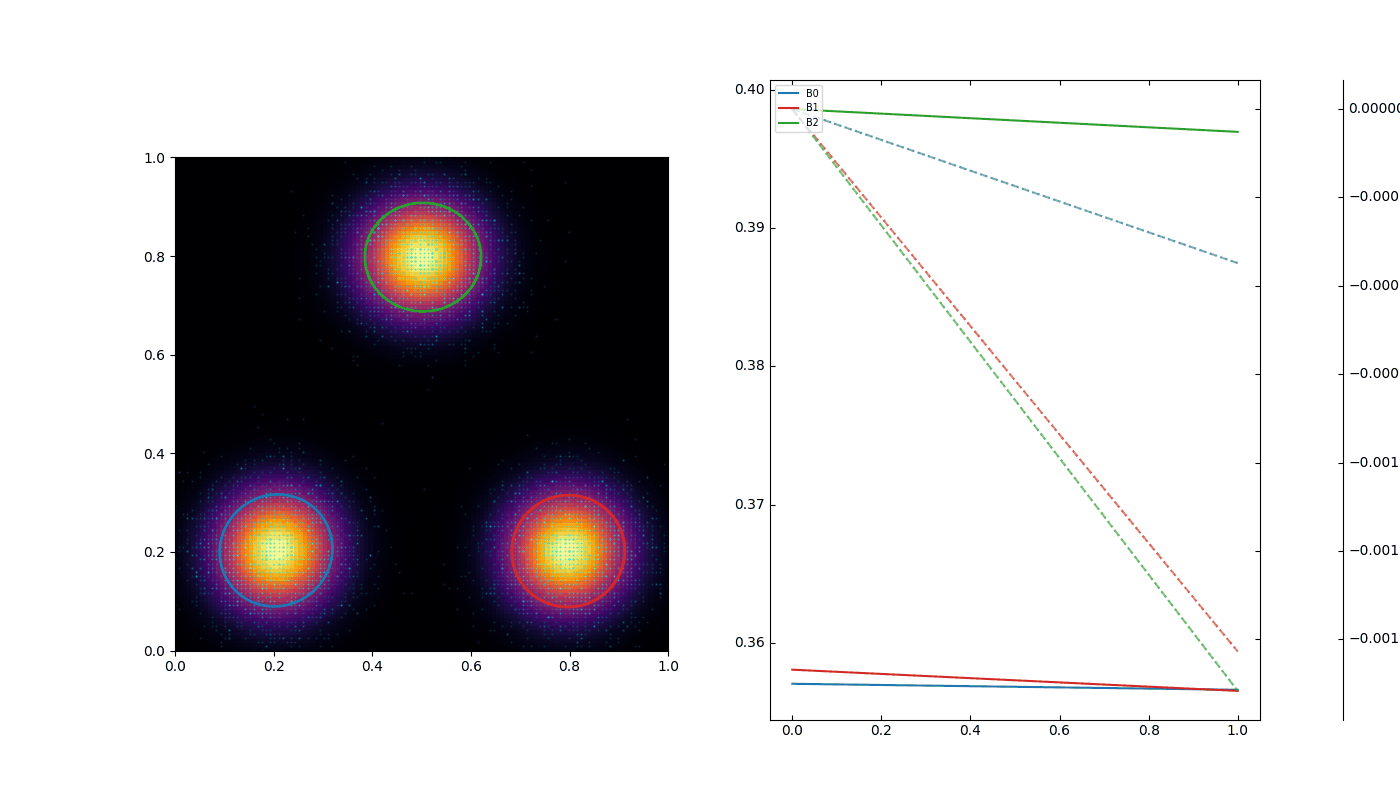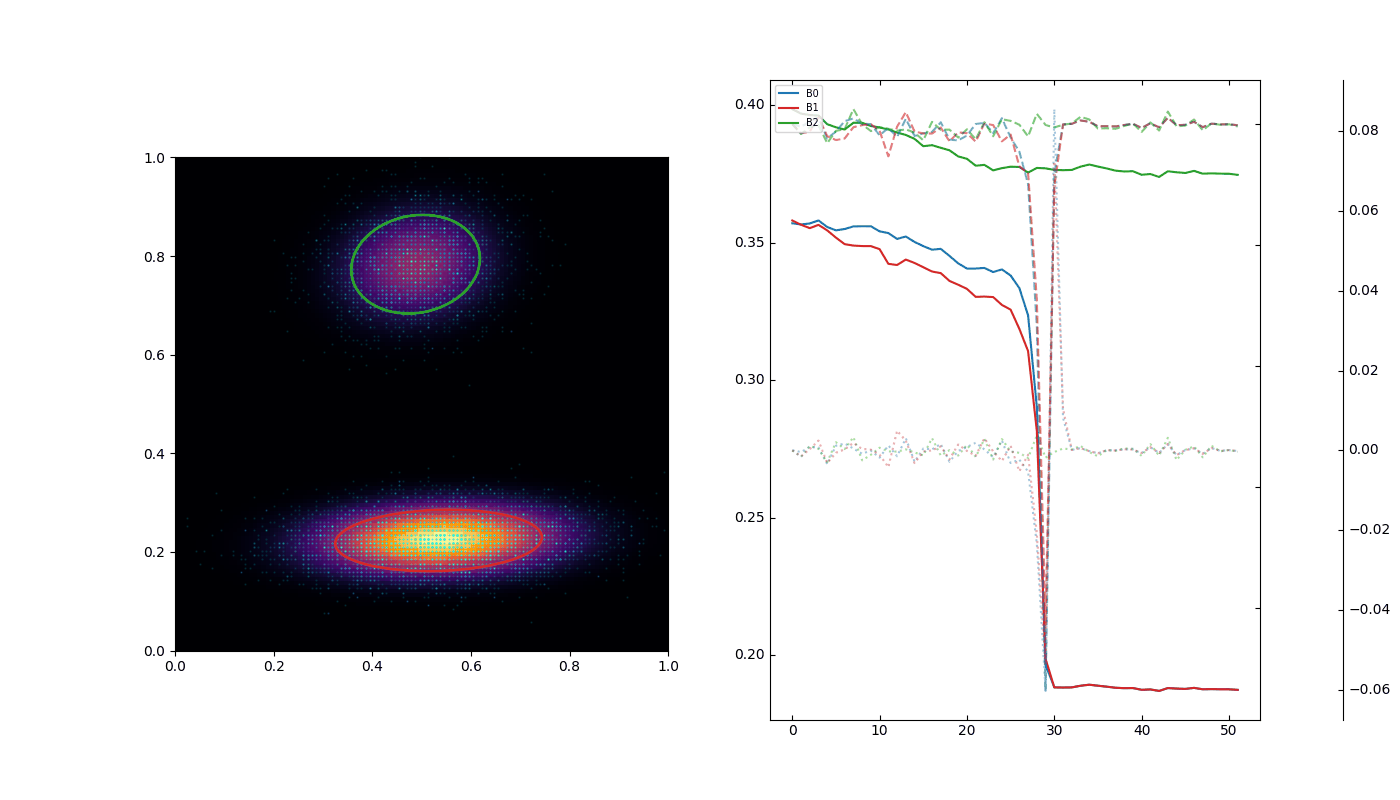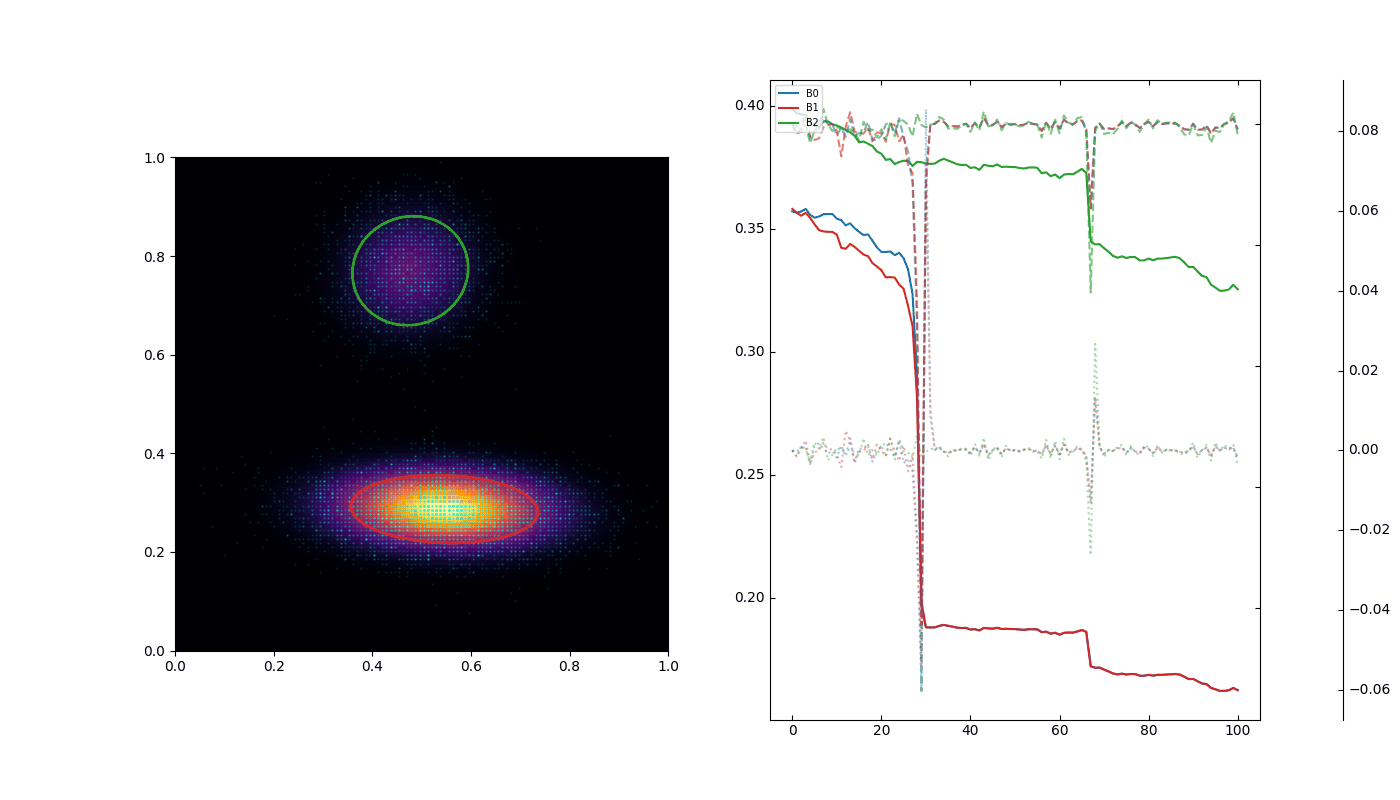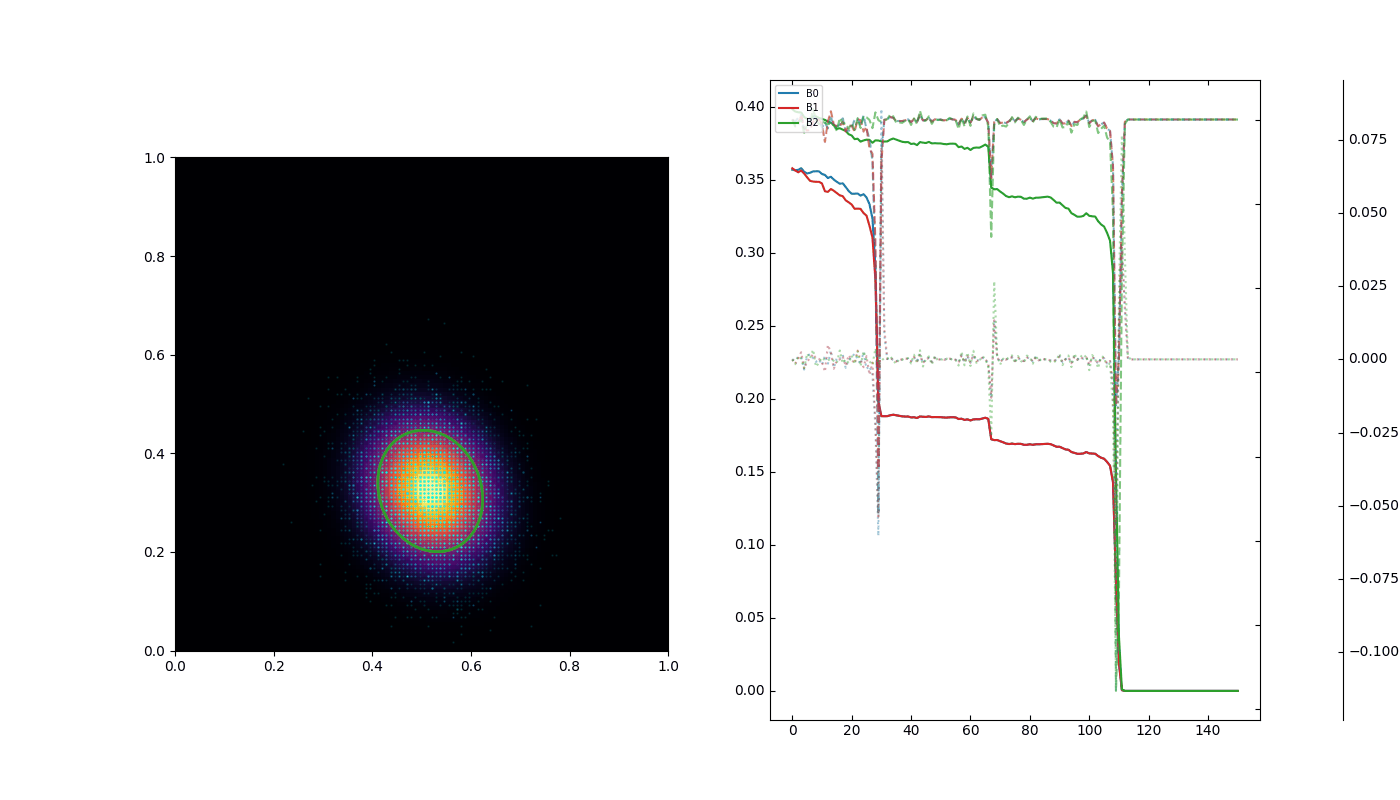
Here, we extend the blob model to include full affine transformations—i.e., the center, scaling, skew, and rotation of each blob—and define a self-consistent iterative update:

1. Particle positions are resampled according to the probability density induced by all blobs.

2. Each blob is updated to maximize the compressibility of its full history relative to the observed particle distribution.

3. This process iterates until a self-consistent configuration emerges.

Blob Representation as Wavefunctions

Each blob \(i\) is represented as a complex-valued wavefunction \(\psi_i(\mathbf{x})\), encoding the center, covariance, and internal phase/frequency structure of the blob: \[\psi_i(\mathbf{x}) = A_i \exp\Big[-\frac{1}{2} (\mathbf{x}-\mathbf{\mu}_i)^\top \mathbf{\Sigma}_i^{-1} (\mathbf{x}-\mathbf{\mu}_i) + i \phi_i(\mathbf{x}) \Big]\] Where:

• \(\mathbf{\mu}_i \in \mathbb{R}^d\) is the blob center.

• \(\mathbf{\Sigma}_i \in \mathbb{R}^{d \times d}\) is the covariance matrix, encoding scaling, skew, and rotation.

• \(\phi_i(\mathbf{x})\) is a local phase function.

• \(A_i\) is a normalization factor.

Total Particle Density from Wavefunctions

The total particle density \(\rho(\mathbf{x})\) is computed from the squared magnitude of the sum of all wavefunctions: \[\psi_{\rm total}(\mathbf{x}) = \sum_i \psi_i(\mathbf{x}), \quad \rho(\mathbf{x}) = |\psi_{\rm total}(\mathbf{x})|^2\] This formulation naturally captures interference effects while ensuring \(\rho(\mathbf{x}) \ge 0\), suitable for particle resampling.

Affine Transformations and Compression

The covariance \(\mathbf{\Sigma}_i\) allows each blob to undergo scaling, skewing, and rotation. Each blob maintains a memory of its past wavefunction parameters \(\mathcal{H}_i\). Candidate updates are evaluated by the Minimum Description Length (MDL) cost of the evolution of the mean, covariance, and phase: \[\mathcal{C}[\mathcal{H}_i \cup (\mu, \Sigma, \phi)] = \text{MDL cost of trajectory evolution}\]

Iterative Self-Consistency

The simulation proceeds through iterative loops analogous to solving Einstein’s equations:

1. Resample Particles: Draw positions \(\{\mathbf{x}_j\}\) from \(\rho(\mathbf{x})\).

2. Update Blobs: Compute the MLE estimate of mean and covariance, adjusted by history cost: \[(\mathbf{\mu}_i^{\text{new}}, \mathbf{\Sigma}_i^{\text{new}}) = \arg\min_{\mu, \Sigma} \Big[ - \sum_j \log \mathcal{N}(\mathbf{x}_j \,|\, \mu, \Sigma) + \mathcal{C}[\mathcal{H}_i \cup (\mu, \Sigma)] \Big]\]

Emergent GR-Like Behavior

Particle trajectories follow geodesics of the emergent density field. High-frequency divergences are automatically suppressed because abrupt changes in \(\mathbf{\Sigma}_i(t)\) are informationally costly. Collapsing blobs are stretched dynamically, producing smooth curvature analogous to spacetime warping in GR. Trajectories far from high-density blobs remain nearly straight, reproducing asymptotically flat space.

Conclusion

By extending Gaussian blobs to full affine transformations and evaluating configurations via compressibility over their histories, we achieve a unified probabilistic emergence of inertia, quantum mechanics, and General Relativity. This demonstrates that spacetime dynamics can be recovered from the informational principle of maximum compressibility.

Simulation Software

• quantum-gravity2.py: Quantum-gravity 2

• Qbitwave python package