2022
We present a constructive proof-of-concept demonstrating that classical geodesic paths on a curved surface can be recovered by minimizing an informational cost functional defined in bitstring. Specifically, we compare Euclidean action minimization with minimization of a phase-coherent spectral entropy computed from local bit-encoded wavefunction segments. We interpret the wavefunction as a minimal description of nature, compressing the underlying information such that smoother, simpler waveforms dominate statistical measure. Without assuming any prior equivalence between geometric and informational principles, we show that both methods select nearly identical paths across a range of noisy, nontrivial geometries. This result supports the hypothesis that classical spacetime dynamics may emerge from an underlying informational principle.
Keywords: Geodesics, Informational Action, Spectral Entropy, Phase Coherence, QBitwave, Quantum Geodesic, Euclidean Action, Minimal Description Length, Discrete Path Optimization
Here, we explore the notion that the wavefunction itself is a compression system for the universe: any set of information can be arranged into many possible wavefunctions, and simple, smooth wavefunctions admit vastly more representations. Thus, smoother, lower-entropy wavefunctions dominate statistical measure, realizing a form of minimal-description principle akin to Kolmogorov complexity but with well-defined size and smoothness constraints.
We investigate whether a purely informational cost functional, defined independently of geometry, can recover classical geodesic behavior. Our approach is algorithmic and discrete: paths are selected step-by-step by minimizing phase-coherent spectral entropy over local execution traces. Remarkably, we find strong agreement between the two resulting paths, suggesting that minimal descriptions naturally encode geodesic structure.
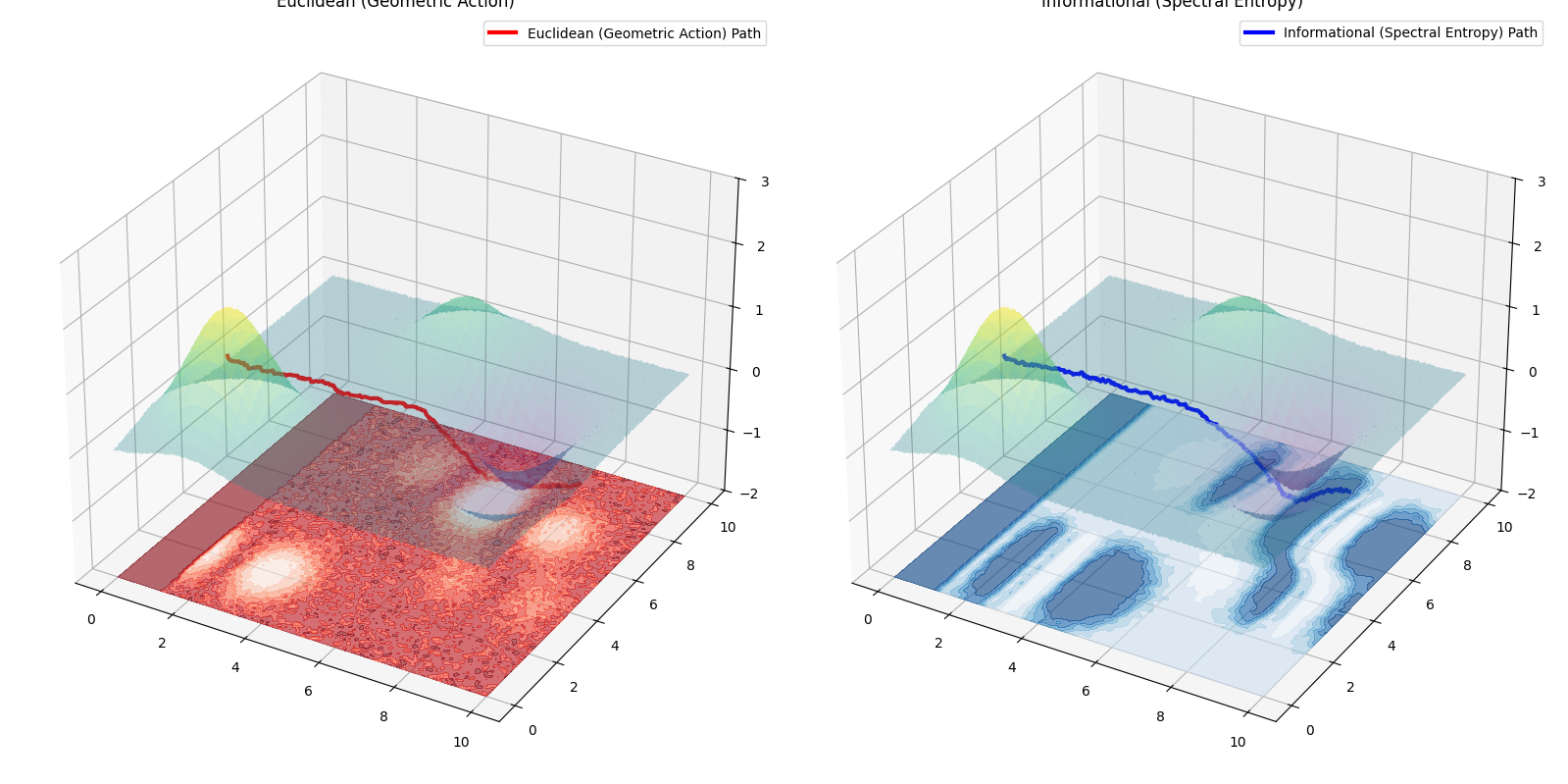
We consider a two-dimensional spatial domain embedded in a three-dimensional height field, representing a curved metric surface. The surface is constructed as a superposition of Gaussian hills and valleys with added stochastic noise. Let \(\phi(x,y)\) denote the surface height. The classical Euclidean action for a path \(\gamma\) proceeding in the \(x\) direction is approximated locally by \[I_E \approx \sum_x \left( \nabla_x \phi \right)^2,\] where the gradient is discretized on a grid. At each step, the next path position is chosen from a local neighborhood to minimize the incremental contribution to \(I_E\).
We propose that the classical trajectory emerges from an underlying principle of Minimal Description. In this framework, the physical path is not determined by geometric distance, but by the efficiency with which the bit-encoded substrate can represent the state. We define the informational action \(S_I\) as the integral of an informational Lagrangian \(\mathcal{L}_I\):
\[S_I = \int_{\gamma} \mathcal{L}_I(\Psi, \dot{\Psi}) \, dt = \int_{\gamma} \left[ \mathcal{H}(\Psi) + \alpha \, \mathcal{D}(\Psi, \dot{\Psi}) \right] dt\]
where the Lagrangian is partitioned into two fundamental terms: the spectral complexity and the phase incoherence.
The first term, \(\mathcal{H}\), quantifies the informational cost to describe the local state. For a discrete bit-segment \(\Psi\), we compute the normalized power spectral density (PSD) via a real Fourier transform. The probability \(p_k\) of a frequency mode \(k\) is given by: \[p_k = \frac{|A_k|^2}{\sum_j |A_j|^2}\] The spectral entropy is defined as: \[\mathcal{H} = -\sum_{k} p_k \log_2 p_k\] Lower entropy corresponds to smoother waveforms, representing a more compressed minimal description.
To ensure the continuity of the emergent description, we introduce a transport cost \(\mathcal{D}\). This term penalizes rapid phase slips between consecutive execution traces. We utilize the complex inner product to measure the overlap between the current state \(\Psi_t\) and the candidate state \(\Psi_{t+dt}\) in Hilbert space: \[\mathcal{D} = 1 - \frac{|\langle \Psi_t | \Psi_{t+dt} \rangle|}{\|\Psi_t\| \|\Psi_{t+dt}\|}\] This formulation is mathematically equivalent to the Fubini-Study metric, defining the infinitesimal distance between points in projective Hilbert space. It effectively imparts informational inertia, favoring descriptions that maintain phase-stability over time. The purpose is to find the optimal wavefunction (maximal compression).
Both methods employ the same local path-finding structure. Starting from a fixed boundary condition, the path advances column by column. At each step, three candidate positions are evaluated, and the one minimizing the respective cost functional is selected. No geometric information is used in the informational method; likewise, no informational quantities appear in the Euclidean action.
Across multiple randomly generated surfaces, the paths selected by Euclidean action minimization and minimal description (QBitwave) are nearly identical. Incorporating phase coherence (\(\mathcal{D}\)) significantly improves alignment, especially in regions with ambiguous local gradients.

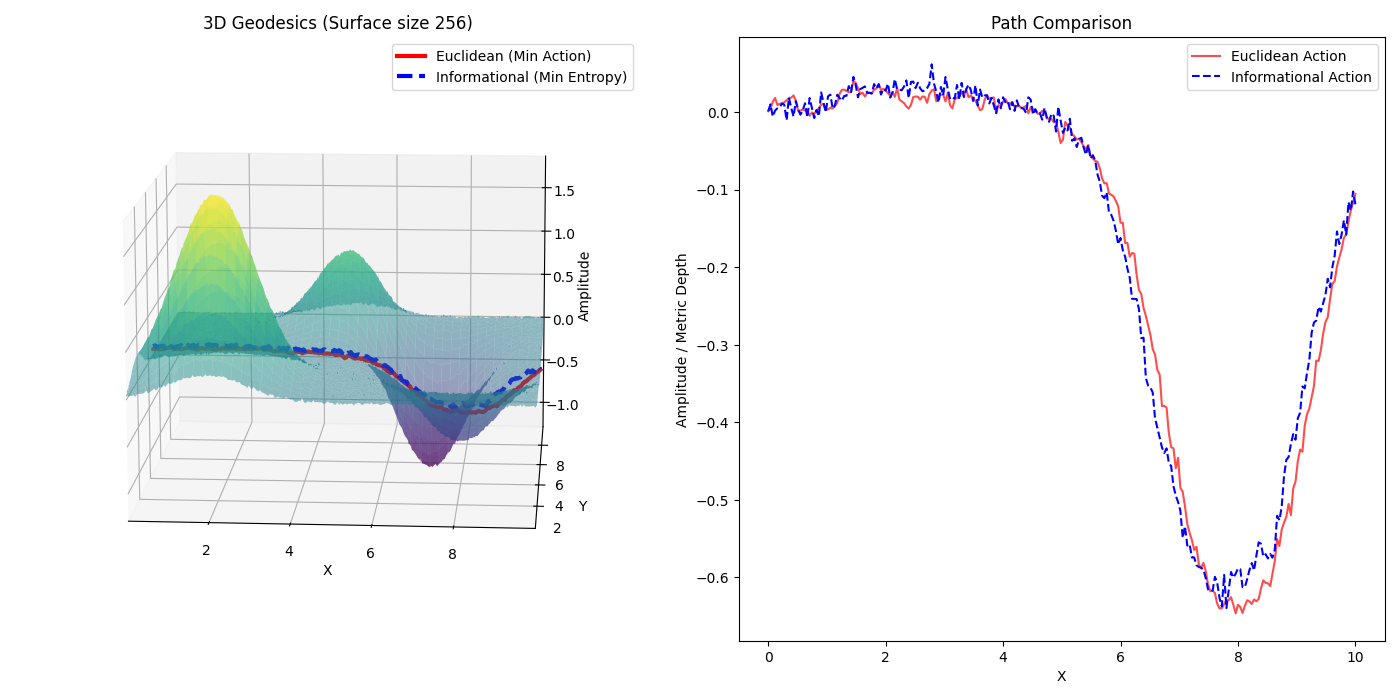
A parameter sweep shows that at low noise, both measures correlate strongly. As noise increases, Euclidean action rises monotonically, while the informational action exhibits a saturation effect due to finite-resolution encoding. This divergence illustrates that informational cost imposes natural cutoffs, reflecting the dominance of smooth wavefunctions as minimal descriptions.
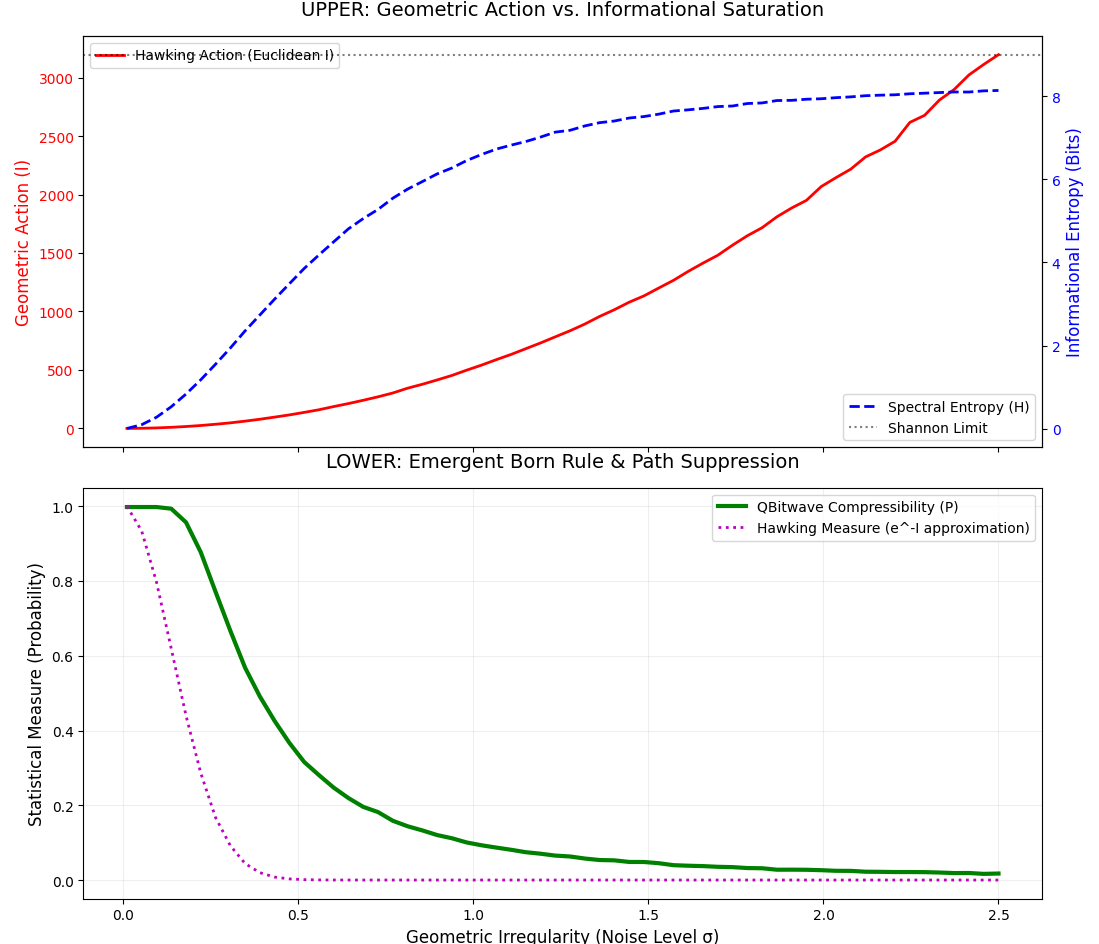
entropy_action_comparison.py. The Euclidean action (red)
increases monotonically with noise. The phase-coherent spectral entropy
(blue) initially tracks the action but saturates at higher noise levels
due to finite-resolution bit encoding and phase-stability effects. The
dashed line represents the compressibility measure of the informational
path, highlighting the minimal-program dominance of smooth, low-entropy
wavefunctions.The observed correspondence suggests that classical geodesics may be understood as paths of minimum informational description. The minimal-description perspective implies that simpler wavefunctions dominate measure and naturally align with Euclidean geodesics.
| Geometric Quantity | Informational Equivalent |
|---|---|
| Potential Energy (\(V\)) | Spectral Entropy (\(\mathcal{H}\)) |
| Kinetic Energy (\(T\)) | Quantum Infidelity (\(\mathcal{D}\)) |
| Action (\(S\)) | Total Description Length (\(\sum \mathcal{L}_I\)) |
| Geodesic | Optimal Compression Trace |
We have demonstrated that minimizing phase-coherent spectral entropy can recover classical geodesic paths.
This result, together with the Entropy-Singularity Lemma, represents two sides of the same coin: regions of vanishing entropy contain no microstructure, while entropy-minimizing trajectories naturally avoid high-entropy, singular configurations.
Taken together, these principles imply that spacetime singularities and divergences are automatically suppressed by the informational structure of the universe.
geodesic_from_information.py: PoC demonstration of informational geodesics on 2D surfaces
phi4_qbitwave_mcmc_2.py: UV suppression in Quantum Field Theory