2018
Building on the identification of zero-entropy singularities (Paper II) and the observation that structures emerge from increasing entropy (Paper III), this paper explores the connection between emergent microstructure density in an information-theoretic view and matter-energy in General Relativity. We implement a probabilistic mapping from information-theoretic bitflips to semiclassical stress-energy, providing a framework in which stochastic matter fields determine the spacetime metric in expectation through Einstein’s equations.
The standard Schwarzschild solution predicts infinite curvature at the singularity. To reconcile these views, we replace the interior solution with a lognormal-shaped distribution of effective curvature, anchored at zero entropy.
In the semi-classical gravity framework, the Einstein field equations are \[G_{\mu\nu} = 8 \pi G \, \langle \hat{T}_{\mu\nu} \rangle,\] where \(\langle \hat{T}_{\mu\nu} \rangle\) is the expectation value of the stress-energy tensor in a given quantum state.
If the singularity corresponds to a zero-entropy state — i.e., no distinguishable microstates, no matter, and no structures — then \[\langle \hat{T}_{\mu\nu} \rangle = 0,\] and the Einstein equations reduce to the vacuum form, \[G_{\mu\nu} = 0,\] describing a well-defined geometry.

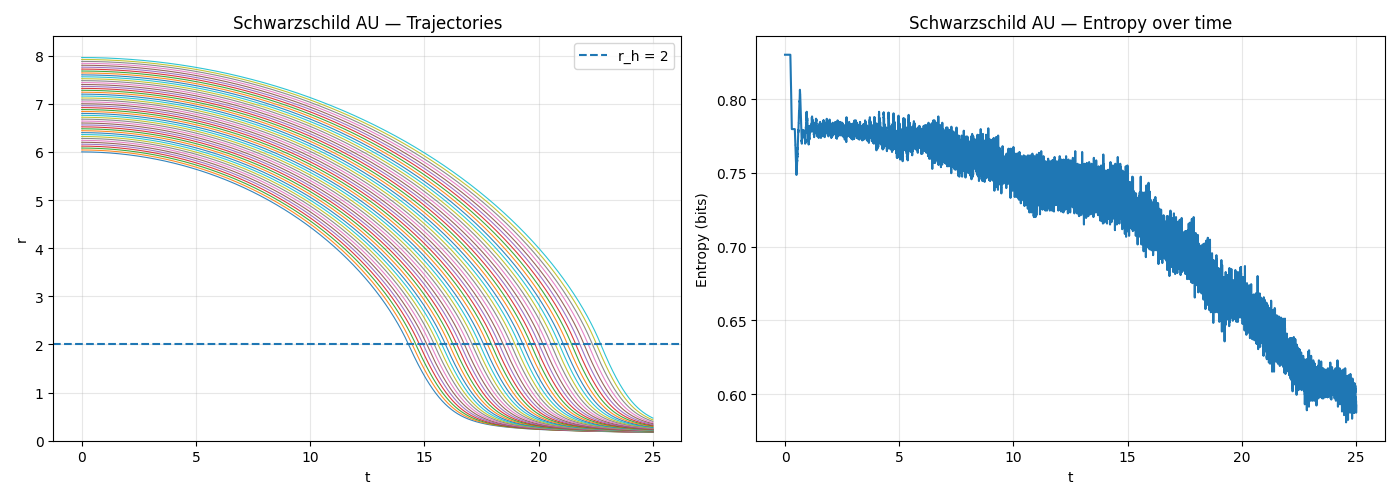
Fitting of lognormal to singularity and event horizon is arbitrary in form, but it has the virtue of dissolving the singularity, preserving information, and yielding well-behaved particle trajectories inside the horizon.
The lognormal distribution suggests that the probability of particles existing rises sharply just outside this zero-entropy state. This means there is a massive concentration of information in the region immediately surrounding the singularity. This could be a testable prediction for a future theory of quantum gravity.
Unlike black holes, where the interior is hidden behind an event horizon, the primordial singularity of our universe is observable indirectly. The early universe leaves its imprint on the cosmic microwave background (CMB) and large-scale structure. From an information-theoretic perspective:
The Big Bang corresponds to a zero-entropy state, where no emergent particles or structures exist.
As entropy increases, geometric structure unfolds, producing particles whose abundances follow a lognormal distribution.
The probability distribution of curvature or matter density peaks at intermediate scales, reflecting the mode of the lognormal distribution.
These statistical peaks could, in principle, leave observable signatures in the CMB, encoding information about the early universe’s geometry.
Thus, while black hole interiors remain inaccessible, the cosmological singularity provides a natural laboratory for testing predictions of the information-theoretic framework.
Even with a perfectly fitted metric derived from emergent microstructure densities, the overall spacetime geometry remains effectively indistinguishable from the classical GR solution at all radii outside an extremely small neighborhood near the singularity. The singularity itself is a zero-entropy fixed point, corresponding to a smooth, information-free vacuum. Any modifications to the metric near the center are secondary refinements and do not alter the essential causal or geometric structure predicted by General Relativity.
Geometric Entropy: The discovery that while total physical entropy increases, the geometric space of a collapsing black hole can be understood as a geometric interpretation of information with decreasing entropy. Conversely, the Big Bang represents increasing entropy.
Emergent Laws: Wavefunctions and General Relativity are emergent features arising from information serving as optimal compression algorithms.
Let worldlines be random paths \(\gamma\) on a manifold \(M\). We define a probability distribution on paths centered on General Relativity (GR): \[\mathbb{P}[\gamma] \propto \exp\!\left( -\frac{1}{2}\int_\gamma \frac{\|a_\gamma(\tau)-a_{\rm GR}(\tau)\|^2}{\sigma^2(\mathcal{I}(x(\tau)))}\, d\tau \right)\] where \(a_\gamma\) is the stochastic 4-acceleration, \(a_{\rm GR}\) is the GR geodesic acceleration, and \(\sigma(\mathcal{I})\) is a scale-dependent noise amplitude depending on a curvature invariant \(\mathcal{I}\) (e.g., the Kretschmann scalar \(K=R_{abcd}R^{abcd}\)).
For any coordinate that shrinks under attraction (such as the radial coordinate \(r\) in Schwarzschild geometry), we evolve the system multiplicatively in proper time: \[\ln r(\tau+\Delta\tau) = \ln r(\tau) + \mu(r)\,\Delta\tau + \sigma(\mathcal{I}(r))\,\sqrt{\Delta\tau}\,\xi\] with \(\xi \sim \mathcal{N}(0,1)\). Consequently, increments of \(\ln r\) are Gaussian, making the radial steps lognormal. The drift \(\mu(r)\) is calibrated so that the most probable trajectory recovers the GR geodesic.
Vanishing entropy corresponds to a collapsing geometry, i.e., a geometric singularity.
If entropy counts accessible microstates, then at the singularity there are none left (\(S \to 0\)). Therefore, the probability of particle emission or fluctuation at the singularity must vanish.
**Entropy as a Function of Curvature**
Let \(I\) be a curvature invariant. We define a coarse-grained entropy \(S(I)\) such that: \[S(I) \ge 0, \quad S(I) \xrightarrow[I\to 0]{} S_0 > 0, \quad S(I) \xrightarrow[I\to \infty]{} 0\] We model this using exponential decay: \[S(I) = S_0 \exp\!\left[-(I/I_P)^m\right], \quad m > 0\] where \(I_P \sim \ell_P^{-4}\) sets the Planck curvature scale.
**Noise Amplitude and Probability Voids**
We set the noise variance proportional to entropy: \(\sigma^2(I) = \kappa\, S(I)\).
Far from the singularity (\(I \ll I_P\)): \(\sigma^2(I) \approx \sigma_0^2\). GR with finite fluctuations is recovered.
Near the singularity (\(I \gg I_P\)): \(\sigma^2(I) \to 0\). Fluctuations are quenched.
The singularity becomes a probability void. There is no stochastic flux into the singular region because there are no available microstates to support existence.
We tie matter to information via a Poisson–lognormal field of bitflips per 4-volume: \[\begin{aligned} N(x)\mid\Lambda(x) &\sim \mathrm{Poisson}(\Lambda(x)) \\ \ln \Lambda(x) &\sim \mathcal{N}\!\big(\mu_\Lambda(x),\, s^2_\Lambda(x)\big) \end{aligned}\] Mapping flips to local stress-energy \(T_{ab}[N]\), we take Einstein-in-expectation: \[G_{ab}(x) = 8\pi G\,\mathbb{E}[T_{ab}[N]] + \text{(finite fluctuation terms)}\]
| Deterministic GR: | \(G_{ab} = 8\pi G\,T_{ab}\) |
|---|---|
| Probabilistic GR: | \(\mathbb{P}[\gamma] \propto \exp\!\left(-\frac{1}{2} \int \frac{\|a_\gamma-a_{\rm GR}\|^2}{\sigma^2(\mathcal{I})}\, d\tau\right)\) |
| Matter Field: | \(N \mid \Lambda \sim \text{Poisson}(\Lambda), \quad \ln\Lambda \sim \mathcal{N}(\mu_\Lambda, s_\Lambda^2)\) |
| Expectation: | \(G_{ab} = 8\pi G\,\mathbb{E}[T_{ab}[N]] + \text{finite cumulants}\) |
| Kinematics: | \(\Delta \ln r = \mu(r)\Delta + \sigma(\mathcal{I})\sqrt{\Delta}\,\xi\) |