2012
Building on the conclusion of Paper II—that collapsing spacetime geometry corresponds to vanishing entropy—we investigate the time-reversed process. Whereas collapsing space corresponds to vanishing entropy, here we hypothesize that the emergence and expansion of spacetime are consequences of increasing entropy. Using a minimal computational model, we evolve a zero-entropy bitstring through random mutations, interpreting its states as geometric structures in three-dimensional space. As the system’s entropy increases, spacetime unfolds, and hierarchical particle-like structures emerge, reproducing key features of matter organization and relative scale invariance. Our results suggest that cosmic expansion can be understood as a geometric manifestation of increasing informational entropy, with complexity and structure arising naturally from simple, initially smooth states.
We define an execution trace \(S_t\), \(t = 0 \ldots n\), where each \(S_t\) is a binary string of fixed length \(L\). Beginning from a state of zero Shannon entropy (an all-zero string), we evolve \(S_t\) via random bit-flip mutations that incrementally increase its entropy.
Each \(S_t\) is geometrically interpreted through various decoding schemes \(D: \{0,1\}^L \to \mathbb{R}^d\). This mapping results in geometric points representing the 3D Spacetime fabric.
We define a hierarchy of elementary structures emerging from the spacetime fabric as follows:
Elementary particles: Defined as pairs of 3D points \((p_1, p_2)\) where the spatial separation between the points is below a threshold.
Atoms: Defined as triplets of elementary particles \((p_1, p_2, p_3)\) such that: \[0 < \text{distance}(p_1, p_2) < \text{threshold}, \quad 0 < \text{distance}(p_2, p_3) < \text{threshold}, \quad 0 < \text{distance}(p_3, p_1) < \text{threshold}\] with distances approximately equal, implying a near-equilateral configuration.
Molecules: Formed when two atoms are sufficiently close. The center of an atom is the geometric mean of its points: \[\text{center(atom)} = \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3}, \frac{z_1 + z_2 + z_3}{3} \right)\] A molecule forms if the distance between two atom centers is below a threshold: \[\text{distance}(\text{center}(\text{atom}_1), \text{center}(\text{atom}_2)) < \text{threshold}\]
The model is minmal and arbitrary, but preserves two key features characteristic of the real universe: (i) the hierarchical structuring of particles, and (ii) the fact that particle sizes do not stretch with the universe, only their mutual distances.
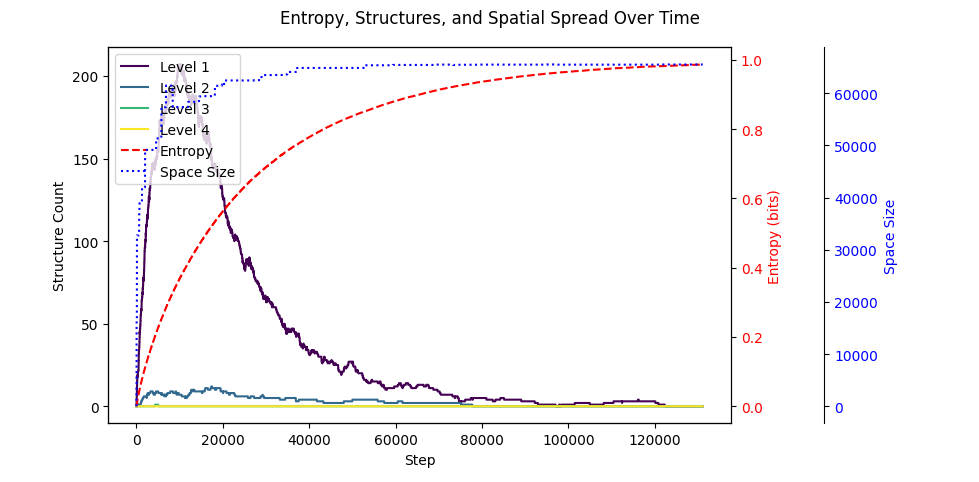
We extract and count the number of these elementary structures at each timestep. As entropy increases through random bit flips, we observe the following:
At zero entropy the spacetime geometry is a point, and no elementary particles emerge.
As entropy increases, the space unfolds exponentially.
At higher entropy, elementary particles, atoms and molecules begin to appear, with their counts following lognormal-like trend.
An alternative definition of emergent particles is given by recursive bit-pattern detection. Here, the execution trace \(S_t\) itself is treated as a one dimensional candidate space of particles, with no explicit geometric mapping required.
Elementary particles: Defined as short substrings \(p \in \{0,1\}^k\) that occur within \(S_t\).
Composite particles: Formed recursively by concatenating previously defined particles. A composite particle \(P\) is valid if it appears in \(S_t\) and if its sub-patterns are recognized particles.
This recursive pattern-matching approach captures the emergence of particles purely from informational redundancy, without reliance on an explicit geometric embedding. The hierarchy is constructed bottom-up: from frequent substrings (elementary particles), to composite concatenations (atoms), to repeated higher-order motifs (molecules).
As with the geometric detection method, two key features of physical reality are reproduced: (i) hierarchical structuring of matter, and (ii) invariance of particle size with respect to global expansion.
By counting the number of recursive particles at each entropy level, we again observe that zero entropy corresponds to no detectable structures, while higher entropy states give rise to exponentially growing numbers of particles whose abundances follow lognormal-like distributions.

A central question in cosmology is why the universe began in such an exceptionally ordered state. Traditional approaches assume that the initial state is not perfectly smooth, constrained only by quantum uncertainty. However, in the informational framework presented here, the apparent necessity of an initially “rough” state is removed.
Beginning from a perfectly smooth, zero-entropy configuration, the universe develops complexity through the unfolding of bitstring information under selection filters. This mechanism naturally produces particle-like microstructures, whose statistical properties follow lognormal distributions. A central implication of this is that the singularity at zero entropy is neither undefined nor pathological.
In this sense, the vanishing-entropy limit implies a form of geometric smoothness that is independent of any particular coordinate system, representation or dynamical description. With no information available to define distinguishable microstructures, the singular state cannot encode physical irregularities, even if classical general relativity breaks down.
The expansion of the universe and the increase of entropy might be two sides of the same coin—two distinct arrangements of the same information. The universe expands because its entropy increases. Expanding universe is geometric interpretation of information of increasing entropy.