2010
Building on the ontological equivalence of physical and informational configurations established in Paper I, we investigate black hole singularities from an information-theoretic perspective, viewing geometric spacetime and the execution trace of a computational simulation as two equivalent interpretations of an underlying informational structure.
Whereas standard General Relativity (GR) cannot be evolved to the point of singularity formation due to numerical divergences and the breakdown of the manifold description, the simulation’s execution trace provides complementary view over the process. This allows us to extrapolate the spacetime description to the actual singularity to the singularity itself. We propose that the “singularity” is not a point of infinite curvature, but rather a state of informational exhaustion, in which the absence of internal variety prevents the emergence of the microstructures we interpret as matter and energy.
The guiding hypothesis is that spacetime geometry and the execution of a simulation can be viewed as complementary descriptions of the same underlying informational structure.
Our central question is whether approaching singularities as information-theoretic phenomena provides new insights into their structure and physical interpretation. To explore this, we develop both analytic reasoning and numerical simulations of collapsing dust clouds.
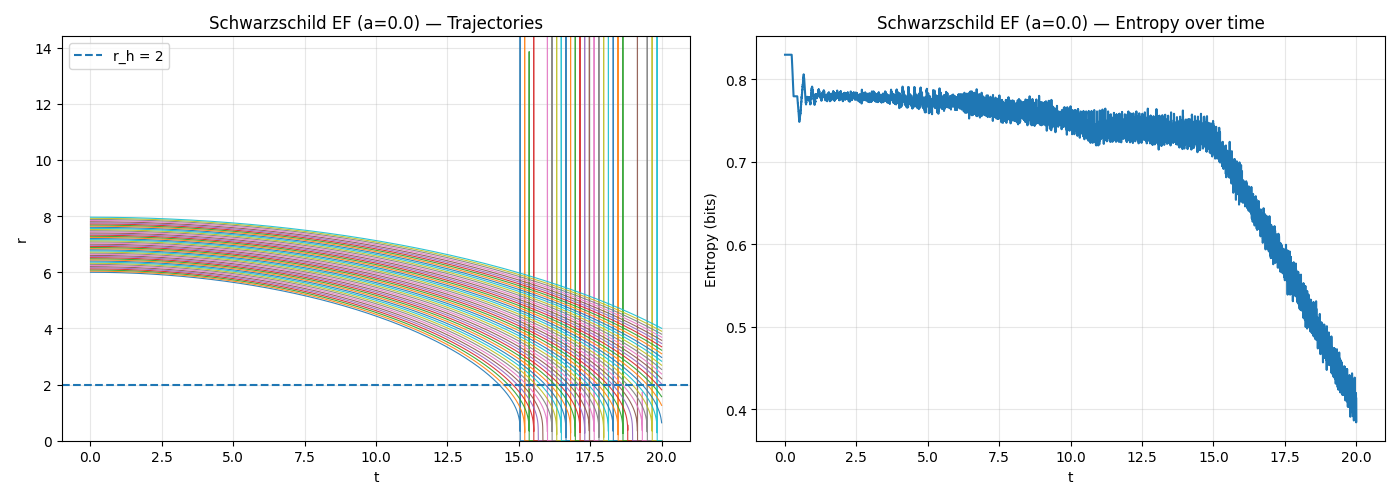
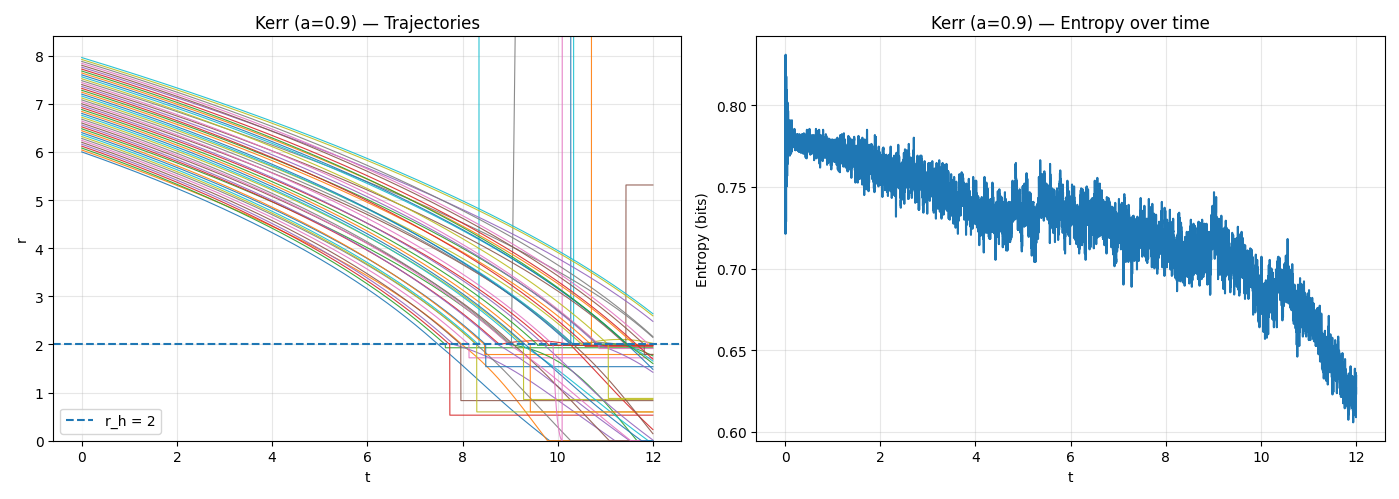
We model black hole evolution through computational simulation. We compute the execution-trace entropy of the discretized particle positions, which captures the number of distinguishable geometric configurations encoded in memory.
Let \(\mathcal{M}\) denote the set of all memory locations in a deterministic computing system. A machine state \(\mathcal{S} \in \mathcal{M}\) is a complete assignment of values to all memory elements. Let \(\mathcal{P} = (I_1, I_2, \dots, I_n)\) be a finite sequence of deterministic instructions, with \(I_k : \mathcal{S} \rightarrow \mathcal{S}\). The execution trace \(\mathcal{T}\) of program \(\mathcal{P}\) is the ordered sequence of states \[\mathcal{T} = (s_0, s_1, \dots, s_n), \quad s_{k+1} = I_{k+1}(s_k).\]
The execution trace encodes all information about the simulated phenomenon. In practice, we focus on the bitstring sub-trace that encodes spatial geometry.
Let a geometric state be encoded as a bitstring \(b \in \{0,1\}^L\), representing the discretized positions of all particles in the dust cloud. Let \[C = \{0,1\}^{3k}\] be the space of 3D configurations. Define \[f : C \to \mathbb{Z}^3, \quad f(b) = (\phi(b_1), \phi(b_2), \phi(b_3)),\] where \(\phi : \{0,1\}^k \to \mathbb{Z}\) decodes fixed-length binary segments. Quantization ensures that the encoding reflects true positional differences, minimizing spurious entropy from floating-point representations.
To quantify distinguishable configurations, we compute the Shannon entropy of the bitstring representation:
\[H(b) = -p_0 \log_2 p_0 - p_1 \log_2 p_1,\]
where \(p_0\) and \(p_1\) are the empirical frequencies of 0- and 1-bits in \(b\).
Over a sequence of states (the bitstring sub-trace), the entropy trajectory reflects the collapse of distinguishable geometric states as particles fall toward the singularity.
We simulated both Schwarzschild (non-rotating) and Kerr (rotating) black holes. All simulations show a monotonic decrease in execution-trace entropy as particles fall inward. Extrapolation indicates that the singularity corresponds to zero entropy state.

Let \(\mathcal{B}_t \subset \{0,1\}^L\) denote the set of bitstrings encoding geometry over a finite time window near \(t\). If \[H(\mathcal{B}_t) \to 0,\] then the set of distinguishable geometric configurations collapses to a single equivalence class under \(f\). That is, the geometry degenerates to a unique configuration.
Our results show a clear divergence between geometric and informational descriptions of gravitational collapse. While the geometric formulation of General Relativity becomes singular and ill-defined, the informational description remains well-behaved: the execution-trace entropy decreases monotonically and converges to zero.
This convergence implies that, near the classical singularity, the set of distinguishable geometric configurations collapses to a single informational state. In this limit, all microstate diversity vanishes (\(W=1\)), and the Shannon entropy is exactly zero. Any faithful geometric decoding of such information yields the same object: a single point.
From this perspective, the singularity is not a region of infinite curvature, but a state of informational exhaustion. The apparent breakdown of spacetime reflects not a physical inconsistency, but the absence of internal informational structure required to support distinguishable geometry, matter, or temporal evolution.
In General Relativity, singularities signal the breakdown of the spacetime manifold. In the information-theoretic view developed here, they instead correspond to perfectly well-defined zero-entropy states. The singularity is therefore not a pathological object, but the simplest possible one: a unique informational configuration whose geometric manifestation is a point.
To encode geometry:
Quantize continuous coordinates: \(\mathbb{R} \to \mathbb{Z}\)
Convert integers to fixed-width binary strings
Concatenate binary segments into a full state bitstring
Entropy is then computed as above. The collapse of this entropy directly reflects the loss of distinguishable structure.