2021
Building on the informational perspective of reality developed in Papers II–V, we investigate ultraviolet divergences in quantum field theory assuming the wavefunction emerges as a minimal, compressible program encoding the underlying bitstring field configuration. High-frequency modes correspond to incompressible states with vanishing amplitude, leading naturally to suppression of divergent contributions. Numerical simulations of a 1D lattice \(\phi^4\) theory demonstrate that amplitude-weighted one-loop integrals remain finite and flat across momentum space, while standard integrals diverge. These results suggest that interpreting quantum fields as emergent, algorithmic structures provides an intrinsic, information-theoretic UV regularization mechanism, obviating the need for conventional cutoffs or counterterms.
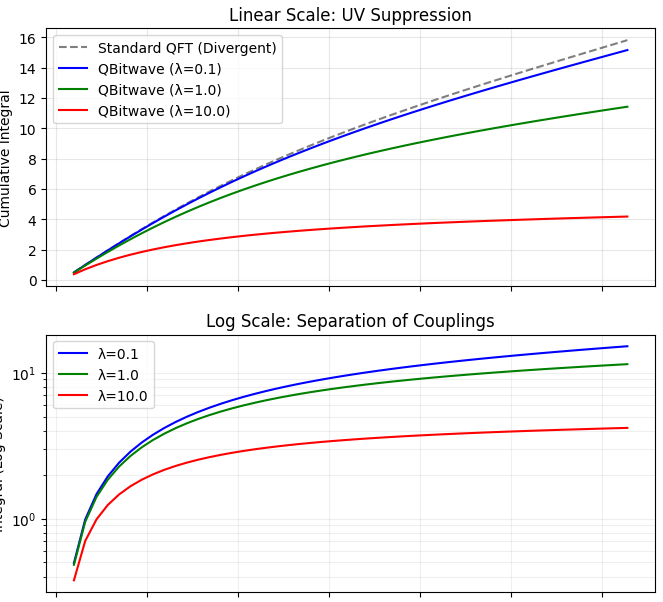
Traditional QFT encounters ultraviolet (UV) divergences in loop integrals. Regularization and renormalization schemes are typically introduced to control these infinities. Here we propose an alternative: treating the wavefunction as an emergent, algorithmic-information-theoretic object. Highly complex (incompressible) field configurations contribute negligibly to physical amplitudes. This naturally suppresses UV contributions, providing a built-in regularization.
We consider a one-dimensional lattice with \(N\) sites, generating field configurations \(\phi(x)\) subject to a \(\phi^4\) interaction: \[\mathcal{L} = \frac{1}{2} (\partial \phi)^2 + \frac{1}{2} m^2 \phi^2 + \frac{\lambda}{4!} \phi^4.\]
Each configuration is mapped to a bitstring encoding the discretized field: \[\phi_i \in [\phi_{\min}, \phi_{\max}] \rightarrow b_i \in \{0,1\}^{\text{bits\_per\_site}}.\]
Given a bitstring \(\mathbf{b}\) , the QBitwave class constructs a normalized complex amplitude array \(\psi(\mathbf{b})\) representing the minimal program reproducing \(\mathbf{b}\) . Compression-based weights are derived from amplitude norms: \[w(\mathbf{b}) = \|\psi(\mathbf{b})\|^2.\]
The one-loop integral for a lattice momentum cutoff \(k_\text{cut}\) is computed as: \[\begin{aligned} I_\text{std}(k_\text{cut}) &= \frac{1}{N_\text{realizations}} \sum_{r=1}^{N_\text{realizations}} \frac{1}{2\sqrt{4 \sin^2(k_\text{cut}/2) + m^2}}, \\ I_\text{info}(k_\text{cut}) &= \frac{1}{N_\text{realizations}} \sum_{r=1}^{N_\text{realizations}} w(\mathbf{b}_r) \frac{1}{2\sqrt{4 \sin^2(k_\text{cut}/2) + m^2}}. \end{aligned}\]
To validate the QBitwave suppression, we performed a Metropolis-Hastings MCMC simulation. Parameters are summarized in Table 1.
| Parameter | Symbol | Value |
|---|---|---|
| Lattice Sites | \(N\) | 128 |
| Encoding Resolution | \(n\) | 8 bits/site |
| Mass | \(m\) | 1.0 |
| Coupling Range | \(\lambda\) | \(\{0.1, 1.0, 10.0\}\) |
| MCMC Steps | \(N_{steps}\) | 1000 |
Figure 1 shows the cumulative one-loop integrals versus momentum cutoff \(k\) :

The bitstring Shannon entropy, averaged over realizations, rises from near zero to close to unity as the lattice modes are sampled:
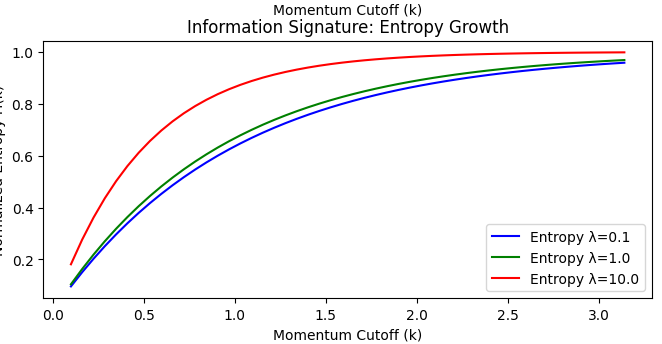
The results suggest that high-momentum modes correspond to incompressible bitstrings with near-zero amplitude in the QBitwave framework. This emergent wavefunction perspective provides a natural, information-theoretic UV regularization without the need for manual counter-terms.
We have demonstrated that interpreting the wavefunction as a compression-based emergent object successfully regulates one-loop QFT divergences. Future research will focus on:
High-Dimensional Scaling: Extending the framework to \(3+1\) dimensions.
Non-Abelian Gauge Fields: Applying weighting to \(SU(N)\) theories.
from qbitwave import QBitwave