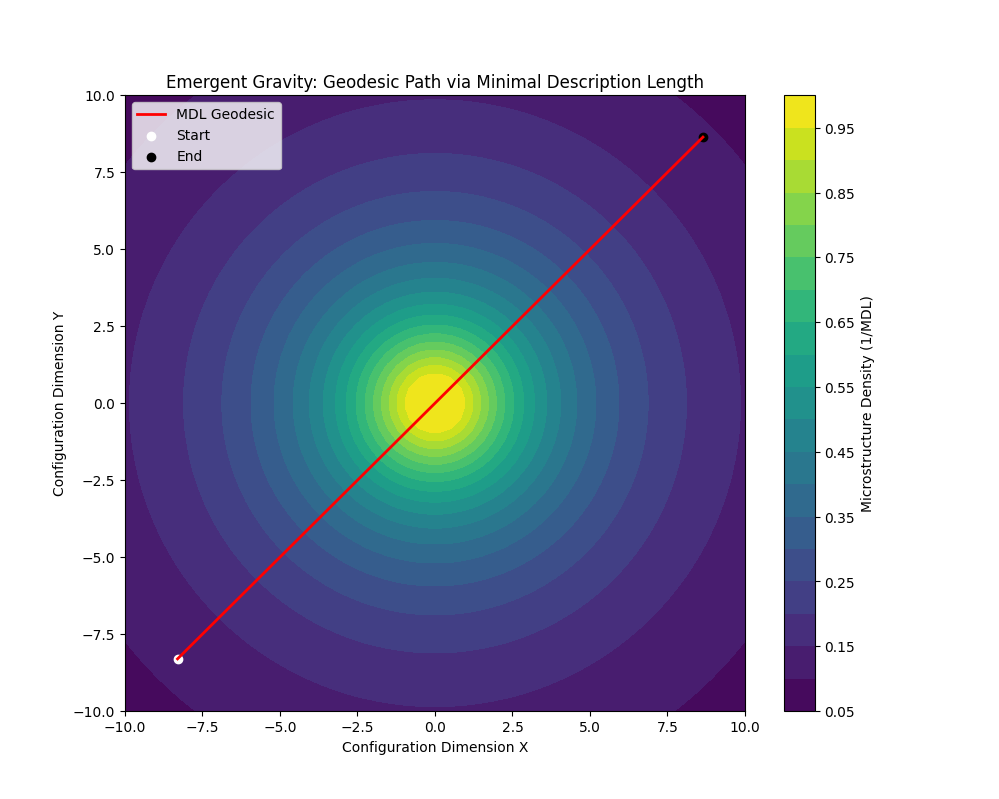
We demonstrate that spacetime curvature and particle geodesics can be derived from a spectral encoding of the universe. By treating the universe as a static ensemble of informational configurations, an observer’s trajectory is biased toward paths that admit efficient spectral compression. The shortest spectral paths correspond to geodesics in a Riemannian manifold, providing a first-principles derivation of gravity from spectral information theory.
General Relativity describes gravity as geometry; in our framework, geometry emerges from information. Configurations of matter and microstructures correspond to patterns in an abstract configuration space \(\mathcal{C}\). Paths through \(\mathcal{C}\) are observer-experienced histories; paths with efficient spectral compression dominate the measure, leading to emergent classical-like physics. We show that minimizing spectral encoding length along observer-compatible paths reproduces geodesic motion.
The metric tensor \(g_{\mu\nu}\) is not fundamental but arises from variations in spectral encoding length: \[g_{\mu\nu} \approx \frac{\partial^2 \mathcal{L}}{\partial x^\mu \partial x^\nu},\] where \(\mathcal{L}\) is the Minimal Spectral Description of the local configuration.
Define the infinitesimal spectral distance \(d\mathcal{L}\) between consecutive states along an observer path \(\gamma\): \[S_{\text{Spectral}} = \int_{\gamma} \mathcal{L}(\text{state}_{t+dt} | \text{state}_t).\] Using the correspondence between second derivatives of spectral encoding and the Fisher information metric \(g_{ij}\): \[S_{\text{Spectral}} \approx \int \sqrt{g_{\mu\nu} \dot{x}^\mu \dot{x}^\nu} dt.\] The path that minimizes spectral description is mathematically identical to a geodesic in Riemannian geometry: \[\frac{d^2 x^\mu}{ds^2} + \Gamma^\mu_{\alpha\beta} \frac{dx^\alpha}{ds} \frac{dx^\beta}{ds} = 0,\] with \(\Gamma\) representing gradients in microstructure density.
A Python-based ensemble simulation demonstrates that agents minimizing \(\mathcal{L}(x_{t+1}|x_t)\) follow Schwarzschild-like trajectories around central motif clusters.

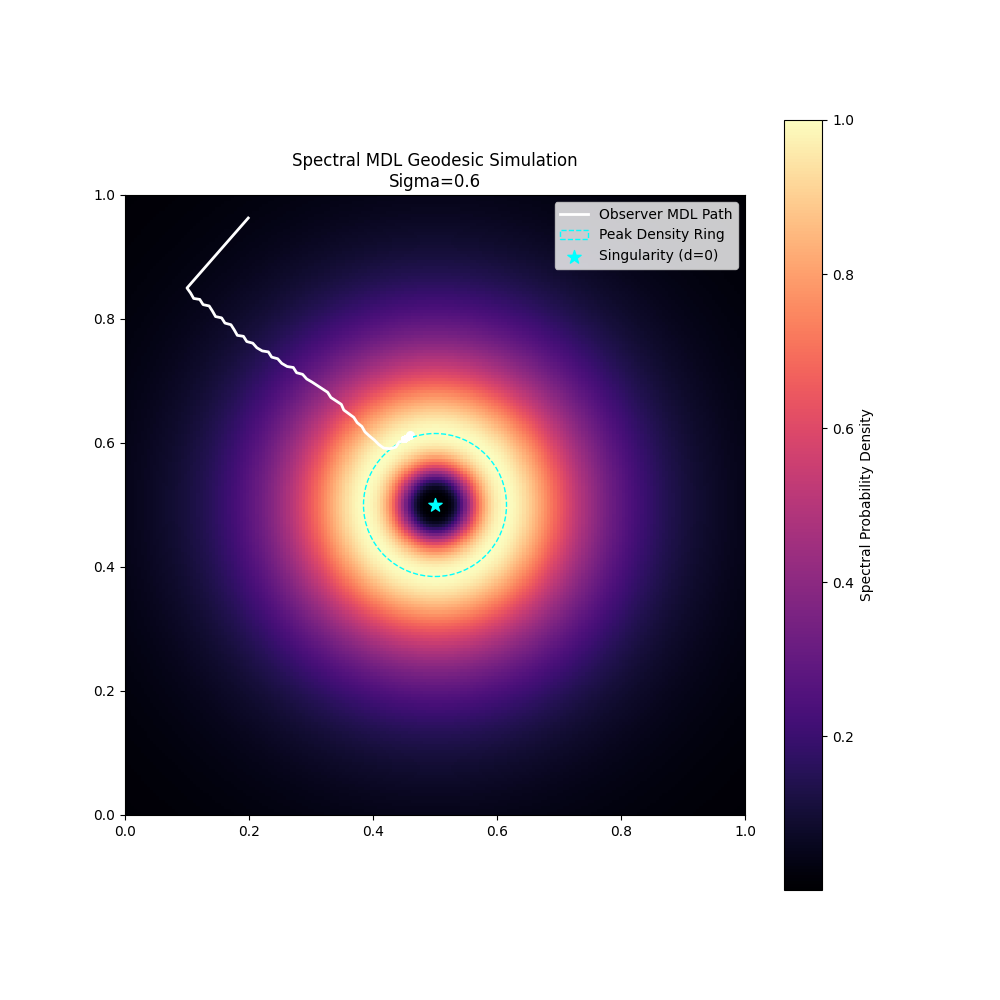
In signal processing, the Nyquist Frequency is the maximum frequency resolvable for a given sampling rate. Analogously:
Sampling Rate: Rate of bit-flips in configuration space \(\mathcal{C}\).
Planck Limit: Maximum frequency representable in the spectral wavefunction \(\Psi\).
Implication: Features smaller than Planck length or faster than Planck time are aliased and cannot exist for observers.
Configurations contain \(n\) bits. Transitions \(s_i \to s_{i+1}\) in a path \(\gamma\) involve bit-flips. Spectral encoding \(\mathcal{L}\) only updates when significant motif changes occur. Observer time emerges from these discrete spectral updates.
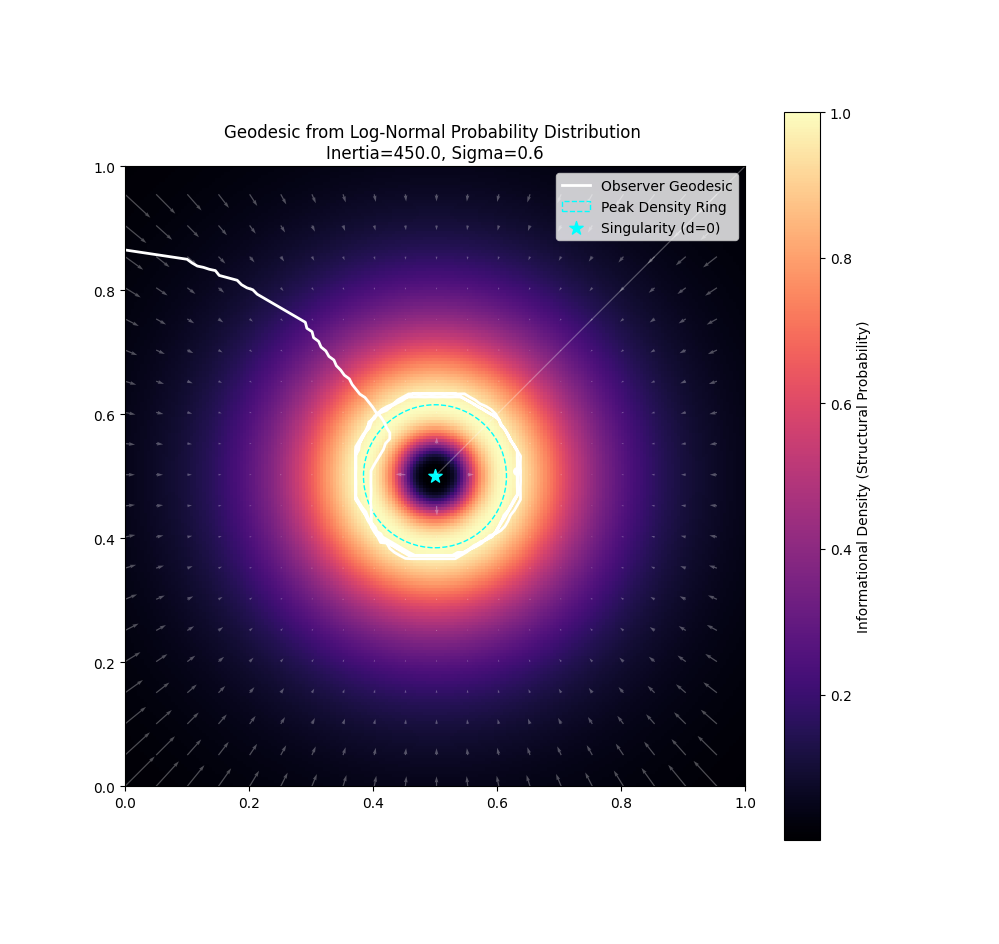
The log-normal distribution of microstructure motifs naturally produces \(1/r^2\) scaling:
Source: Clusters of reusable motifs represent masses.
Radial Distribution: Configurations that reference the cluster increase with sphere surface area: \(A=4\pi r^2\).
Consequence: Probability pressure toward motifs falls as \(1/r^2\), reproducing classical gravitational scaling.