2023
We show that the dominance of compressed observer descriptions follows from a purely combinatorial argument.
Let the total information budget of the universe be fixed at \(N\) bits. Consider an observer \(O\) whose identity can be fully specified by a minimal description of \(k\) bits, with \(k \leq N\). The remaining \(N-k\) bits correspond to degrees of freedom that do not affect the observer’s identity.
We assume a uniform measure over the space of all \(2^N\) possible bitstrings of length \(N\).
An observer \(O\) is realized whenever its \(k\) defining bits are embedded into an \(N\)-bit string, regardless of the values of the remaining \(N-k\) bits. The total number of distinct realizations of \(O\) is therefore
\[\Omega(O \mid N, k) = \binom{N}{k} \, 2^{\,N-k},\]
where:
\(\binom{N}{k}\) counts the number of ways to choose the locations of the \(k\) defining bits,
\(2^{N-k}\) counts the number of possible assignments of the remaining unconstrained bits.
Given the uniform measure over all \(2^N\) bitstrings, the probability that a randomly selected \(N\)-bit configuration instantiates observer \(O\) is
\[P(O \mid N, k) = \frac{\Omega(O \mid N, k)}{2^N} = \binom{N}{k} \, 2^{-k}.\]
This expression is exact and involves no uncomputable quantities.
For fixed \(N\), consider two observers \(O_1\) and \(O_2\) with minimal description lengths \(k_1 < k_2\). The ratio of their probabilities is
\[\frac{P(O_1)}{P(O_2)} = \frac{\binom{N}{k_1} \, 2^{-k_1}}{\binom{N}{k_2} \, 2^{-k_2}}.\]
In the regime \(k \ll N\), we may use the approximation
\[\binom{N}{k} \approx \frac{N^k}{k!},\]
yielding
\[P(O \mid N, k) \approx \frac{N^k}{k!} \, 2^{-k}.\]
This probability decreases rapidly with increasing \(k\). Consequently, observers admitting shorter descriptions occupy an exponentially larger fraction of the configuration space.

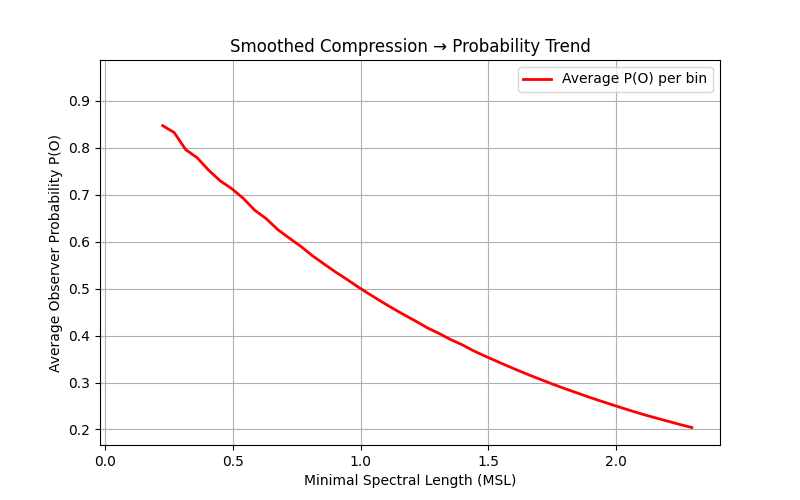
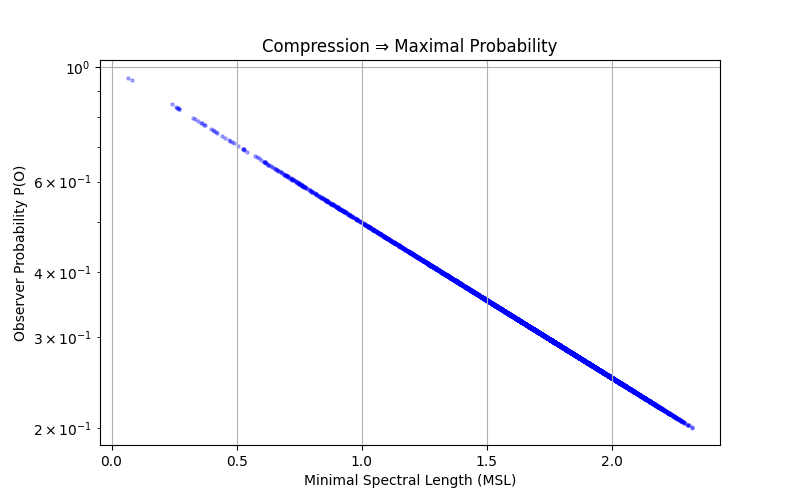
This result establishes that compression implies maximal probability as a direct consequence of combinatorics. No appeal is made to Kolmogorov complexity, Solomonoff induction, or heuristic notions of simplicity. The minimal description length \(k\) may be continuous and physically defined (e.g., via spectral support of a wavefunction) and only mapped to discrete bits after coarse-graining.
In the \(IaM^e\) framework, \(k\) corresponds to the Minimal Spectral Length required to encode the observer. The wavefunction provides the analytic representation achieving this minimal description, and probabilistic weighting arises from the number of compatible microscopic realizations.
For a fixed information budget, observer configurations with minimal description length dominate the measure by necessity. The emergence of compressed, wave-like physical laws therefore follows from exact counting, not heuristic principles or uncomputable complexity measures.